對半檢索算法

最近一個項目，用到了非常古老、且非常高效的對半檢索算法，這次第二次使用這個算法模型進行工程，上一次是6年前

關於

對半檢索算法，是複雜的集合對象環境中，快速找出一個對象的快速搜索算法，適用於分治原則，對數據進行排序。

在查找時，集合中的對象將會被分配一個鍵，鍵總數是2的次方，檢索時，欲查找的對象將會和集合中的中間點比對，如果大於鍵值，那麼該對象則會被保留，剩下的會被拋棄，直到集合中只剩下一個對象。

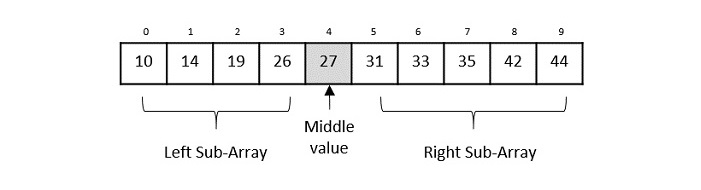
假設我們要適用對半檢索算法找出對象31

首先，我們需要用這個方程式來找出中間值

mid = low + (high - low) / 2

0 + (9 – 0 ) / 2 = 4 (integer value of 4.5). 所以，中間值是4.

我們找出的比較存儲位4的值是27,不匹配。因為我們要查找的值大於27，所以，我們知道目標一定處於數列的上部。

進行修改，將low 修改為 mid + 1，再進行中間值查找

low = mid + 1
mid = low + (high - low) / 2

現在，新結果找出的中間值是7，

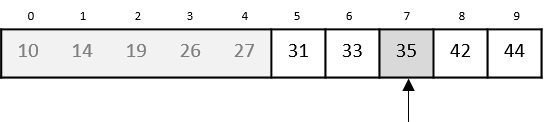
顯然7不是我們的目標，但進一步縮小的目標範圍，目標應該在下部

所以，再次計算中間值，這次是5

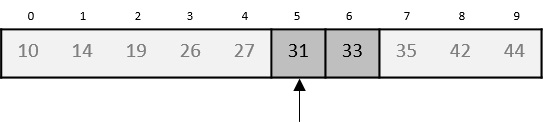
命中！結論是目標值存儲在集合中5這個位置。

範例

Procedure binary_search
   A ← sorted array
   n ← size of array
   x ← value ot be searched

   Set lowerBound = 1
   Set upperBound = n 

   while x not found

      if upperBound < lowerBound 
         EXIT: x does not exists.

      set midPoint = lowerBound + ( upperBound - lowerBound ) / 2

      if A[midPoint] < x
         set lowerBound = midPoint + 1

      if A[midPoint] > x
         set upperBound = midPoint - 1 

      if A[midPoint] = x 
         EXIT: x found at location midPoint

   end while

end procedure

C下的實現

#include <stdio.h>

#define MAX 20

// array of items on which linear search will be conducted. 
int intArray[MAX] = {1,2,3,4,6,7,9,11,12,14,15,16,17,19,33,34,43,45,55,66};

void printline(int count){
   int i;

   for(i = 0;i <count-1;i++){
      printf("=");
   }

   printf("=\n");
}

int find(int data){
   int lowerBound = 0;
   int upperBound = MAX -1;
   int midPoint = -1;
   int comparisons = 0;      
   int index = -1;

   while(lowerBound <= upperBound){
      printf("Comparison %d\n" , (comparisons +1) ) ;
      printf("lowerBound : %d, intArray[%d] = %d\n", 
        lowerBound,lowerBound,intArray[lowerBound]);
      printf("upperBound : %d, intArray[%d] = %d\n", upperBound,upperBound,intArray[upperBound]);
      comparisons++;

      // compute the mid point 
      // midPoint = (lowerBound + upperBound) / 2;
      midPoint = lowerBound + (upperBound - lowerBound) / 2;    

      // data found
      if(intArray[midPoint] == data){
         index = midPoint;
         break;
      }else {
         // if data is larger 
         if(intArray[midPoint] < data){
            // data is in upper half
            lowerBound = midPoint + 1;
         }
         // data is smaller 
         else{           
            // data is in lower half 
            upperBound = midPoint -1;
         }
      }               
   }
   printf("Total comparisons made: %d" , comparisons);
   return index;
}

void display(){
   int i;
   printf("[");

   // navigate through all items 
   for(i = 0;i<MAX;i++){
      printf("%d ",intArray[i]);
   }

   printf("]\n");
}

main(){
   printf("Input Array: ");
   display();
   printline(50);

   //find location of 1
   int location = find(55);

   // if element was found 
   if(location != -1)
      printf("\nElement found at location: %d" ,(location+1));
   else
      printf("\nElement not found.");
}

輸出結果

Input Array: [1 2 3 4 6 7 9 11 12 14 15 16 17 19 33 34 43 45 55 66 ]
==================================================
Comparison 1
lowerBound : 0, intArray[0] = 1
upperBound : 19, intArray[19] = 66
Comparison 2
lowerBound : 10, intArray[10] = 15
upperBound : 19, intArray[19] = 66
Comparison 3
lowerBound : 15, intArray[15] = 34
upperBound : 19, intArray[19] = 66
Comparison 4
lowerBound : 18, intArray[18] = 55
upperBound : 19, intArray[19] = 66
Total comparisons made: 4
Element found at location: 19

本文簡譯自Tutorialspoint的一篇文章